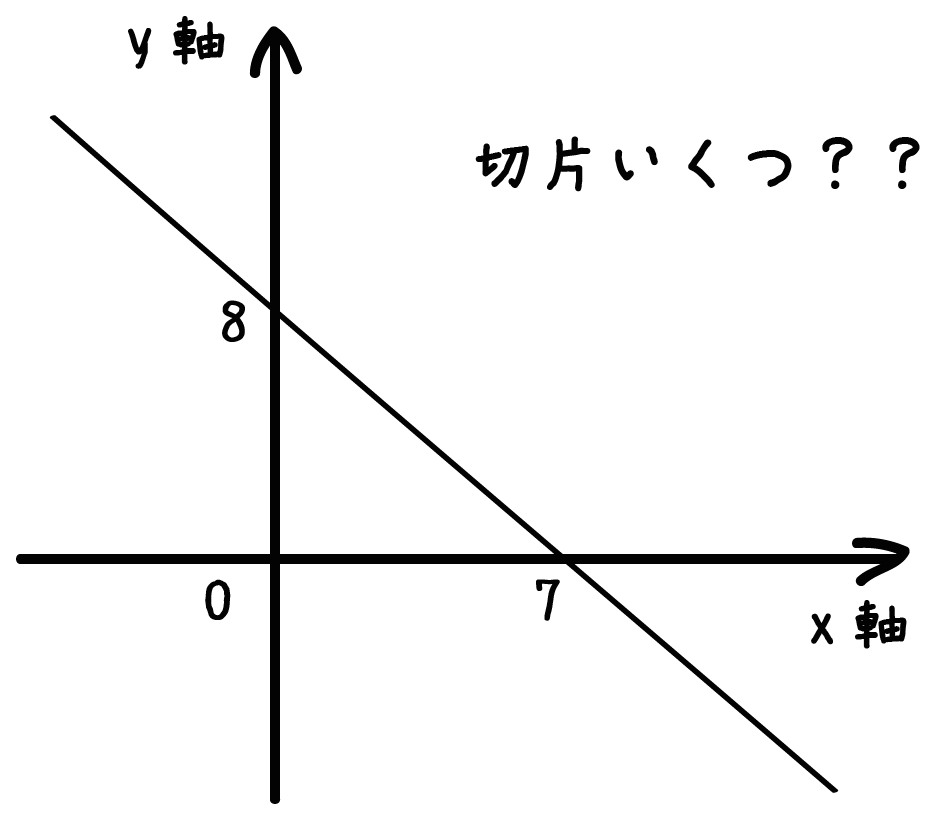
中2数学 一次関数の切片を求める2つの方法 Qikeru 学びを楽しくわかりやすく
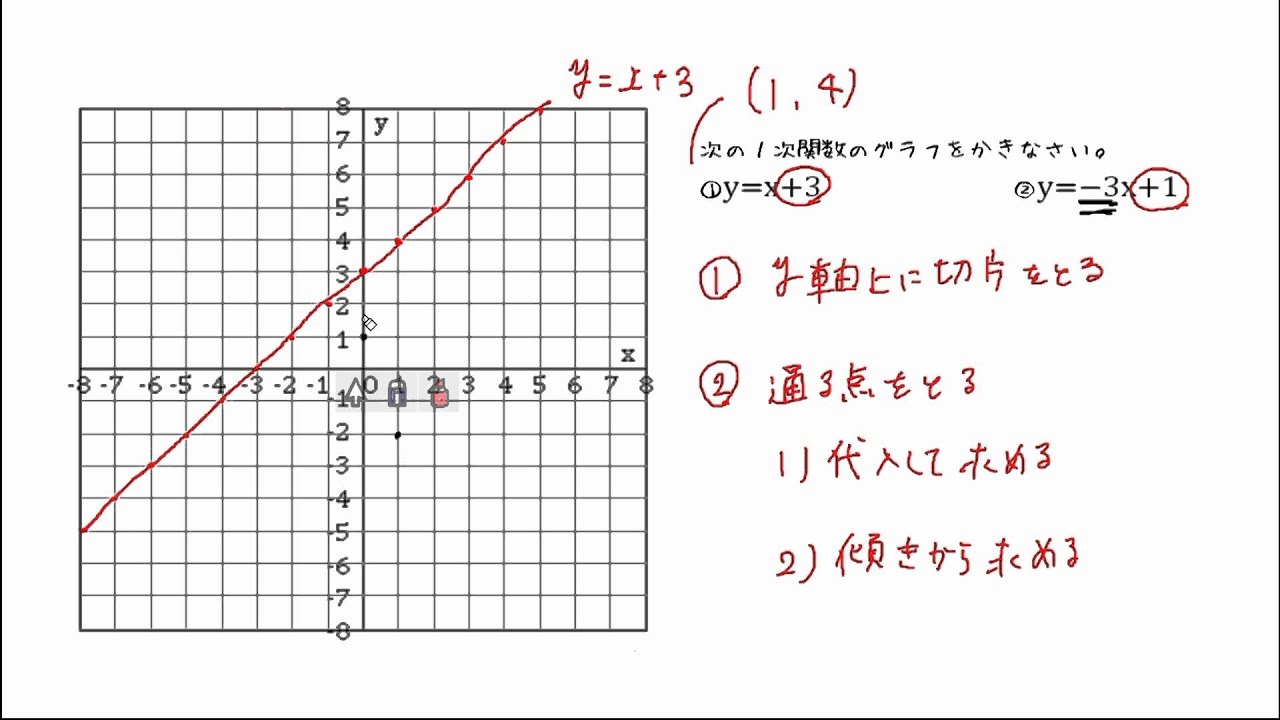
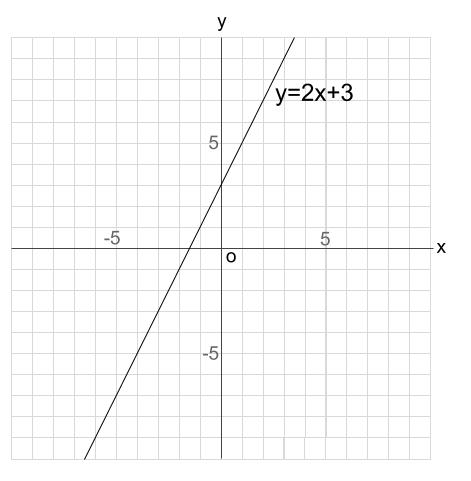
また， 1次関数のグラフを利用して，連立1 次方程式を解くには， 1次関数をみたすすべて の点(x, y)は一つの直線上にあり，逆にその直 線上のすべての点が1次関数をみたすというこ とを理解できていないと納得はできないだろ う。中2数学。「y = 2x 3」のグラフをかきなさい。うわ「1次関数のグラフ」、かき方が分からん（ガクッ）おや、中学生が倒れそう。立て、立つんだトォォォォ～ッ！ オール5家庭教師、見参ッ！ グラフなんて一瞬でかける！ コツを無料公開だ。
1次関数 グラフ 求め方
1次関数 グラフ 求め方- まずは四次関数のグラフの概形について，非常に大雑把な特徴を解説します。 以下，四次の係数 a a a が正であるような四次関数について考えます。 四次関数 y = a x 4 b x 3 c x 2 d x e y=ax^4bx^3cx^2dxe y = ax4 bx3 cx2 dxe のグラフの概形 特徴1．上から 1次関数のグラフが苦手でワークをやっているのですが 画像の矢印の部分が何でマイナスになるのかわかりません。 この式の答えが3分の7になるみたいなのですが、なんで3分の7になるのかもわかりません。 誰か分かりやすく教えて下さい。
1
必要なpackageをインストール 必要なpackageは以下 pip packageを管理するためのpackage; 単元 1次関数,1次関数の利用, 「授業の予習復習 テスト対策 受験対策に」, 学年 中学全学年, キーワード 中学生,中学2年生,数学,中間テスト,期末テスト,math 定数関数・1次関数 a, cを定数として、関数y=axcのグラフは直線になります。これを直線y=axcといい、y=axcをこの直線の方程式といいます。 このように、yがxの1次式で表される関数を1次関数といいます。 ここでa=0のとき、y=cとなりxの値に関係なくyの値は常に一定となります。
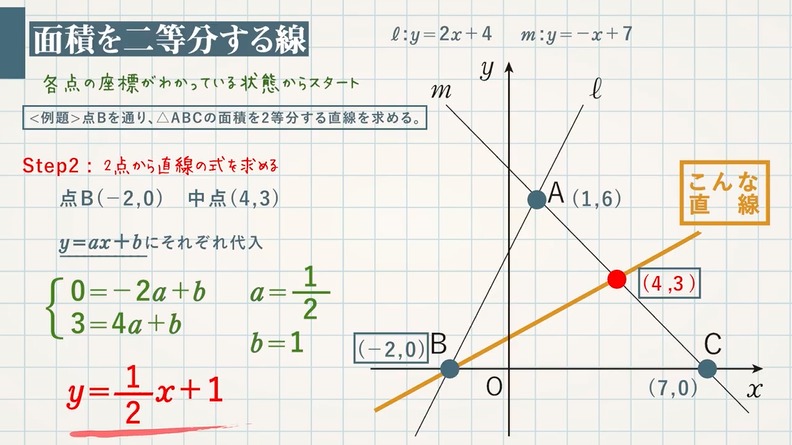
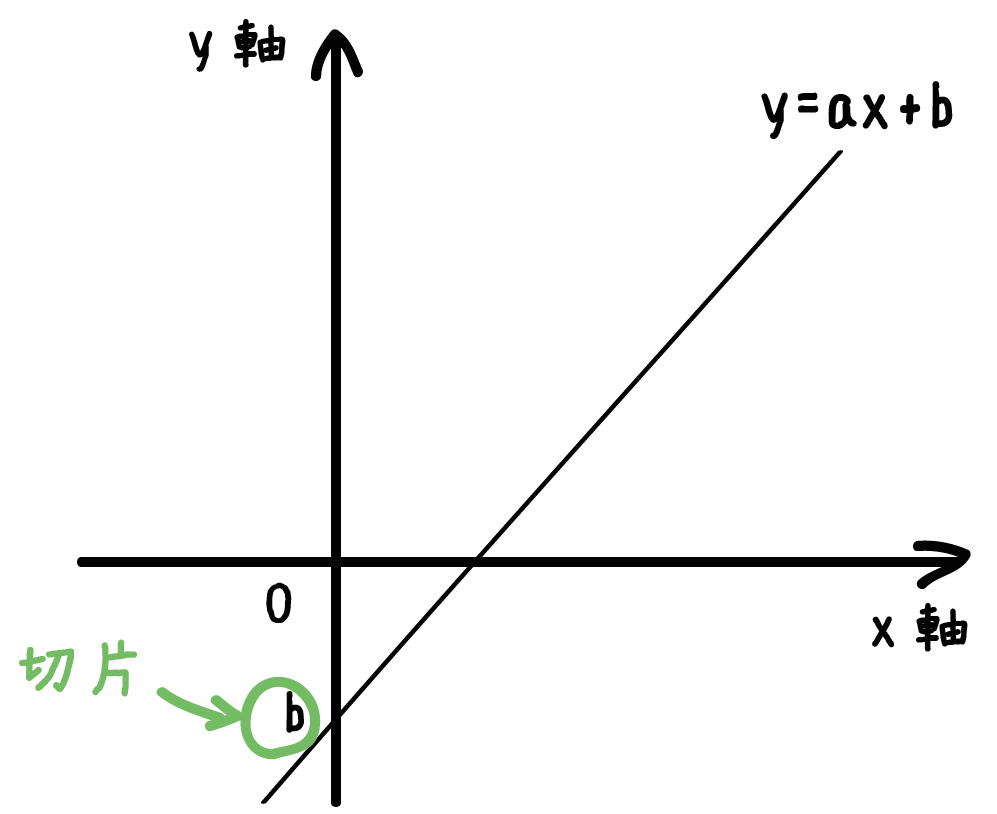
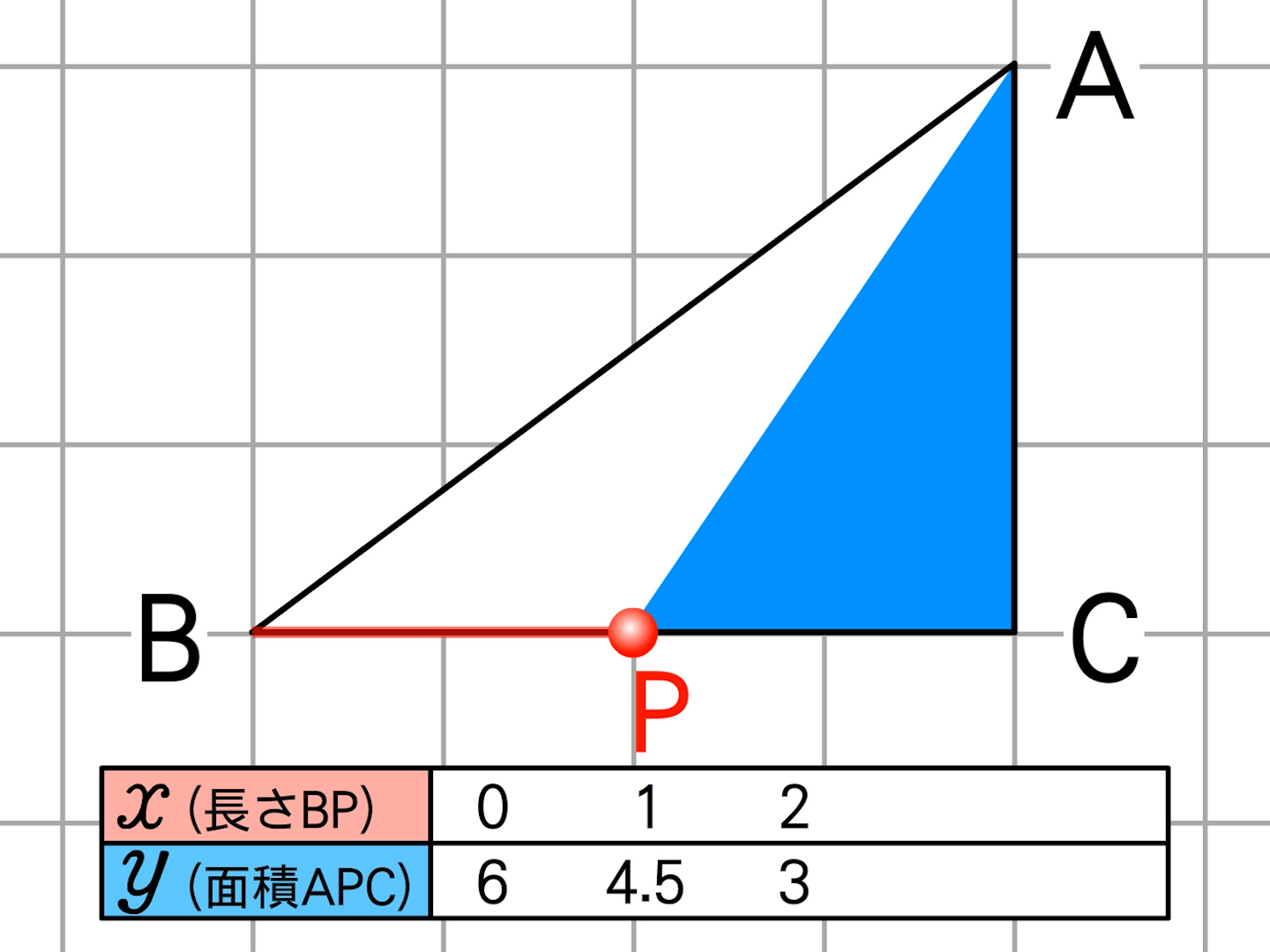
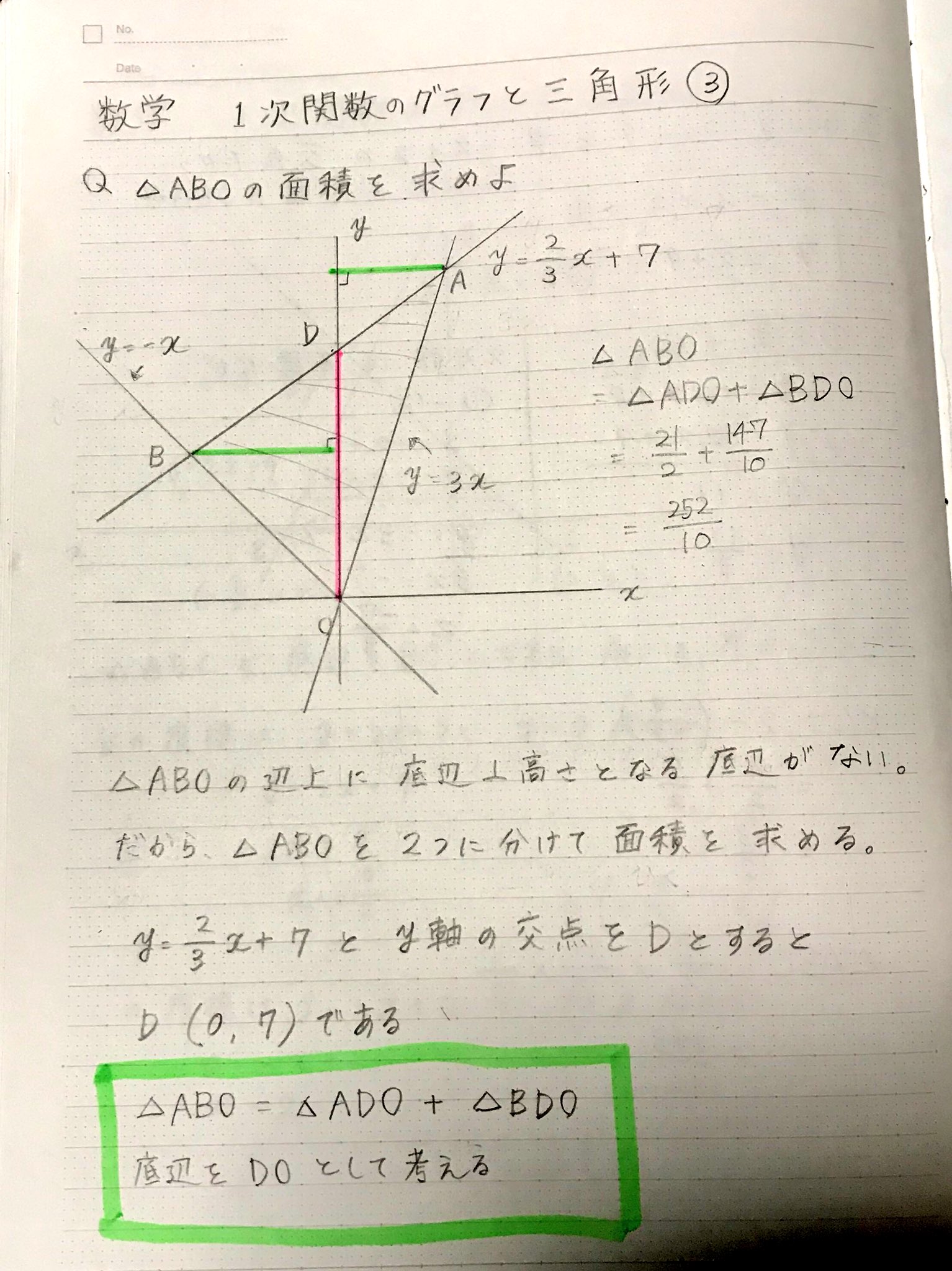
この関数のグラフ {(,,,) = (,,)} は、 (n 1)次元ユークリッド空間 R n1 において超平面（ 余次元 （英語版） 1 のアフィン部分空間）を描く。このような函数に対しても、上に述べたことは（平面における各概念の高次元における適当な対応物を考えることに1次関数のグラフでは，傾きと切片がポイントになります。 ここで紹介している内容は17年3月時点の情報です。 ご紹介している内容・名称等は変わることがあります。 ※ このQ&Aでは、 「進研ゼミ中学講座」 会員から寄せられた質問とその回答の一部をこちらの記事で1から解説をしていまず。 一次関数が苦手だという方はまずはこちらの記事で復習しておいてください。 それでは、次の問題について解き方を順に確認していきましょう。 一次関数面積を求め方の手順
1次関数 グラフ 求め方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
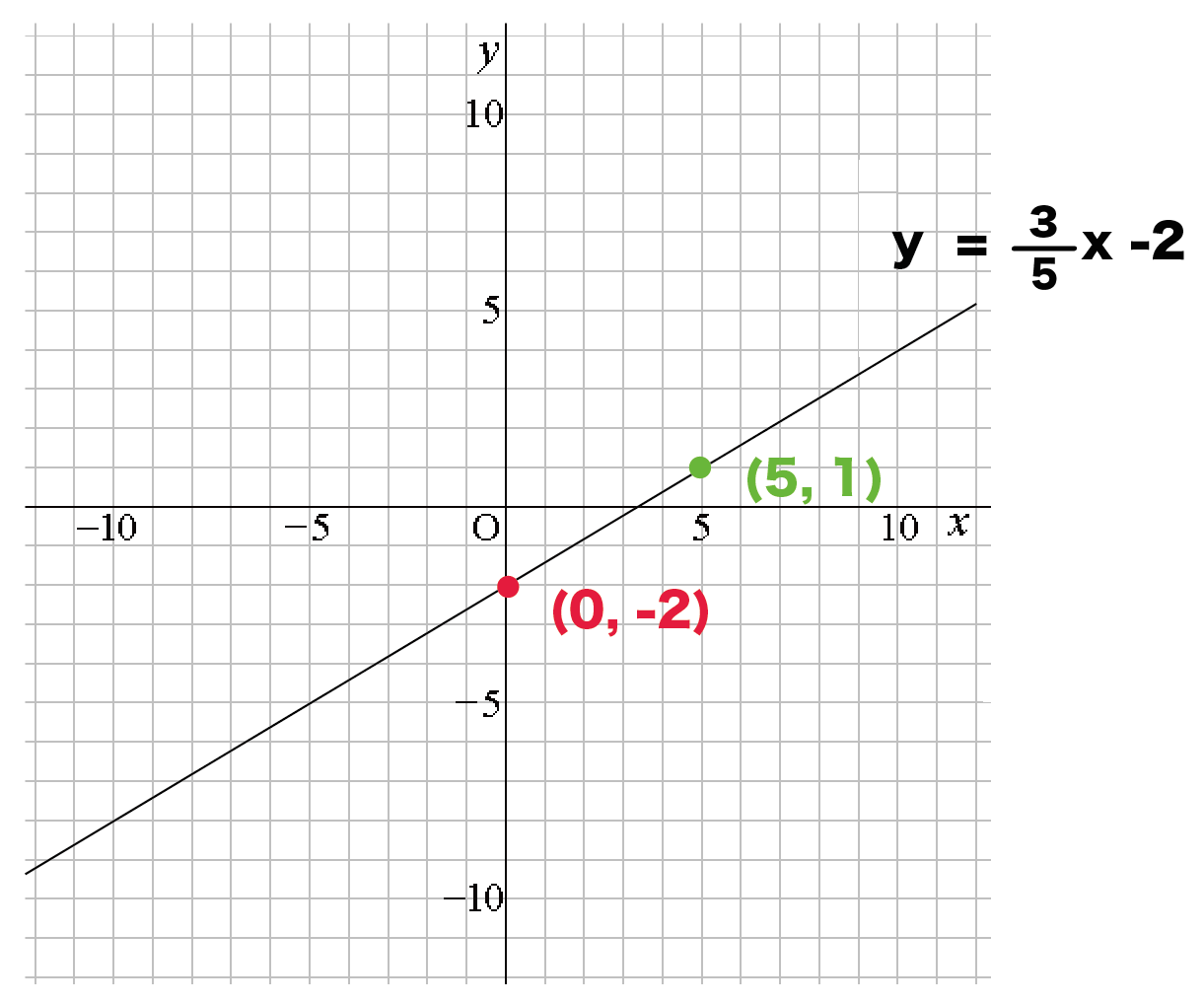 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
「1次関数 グラフ 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 | 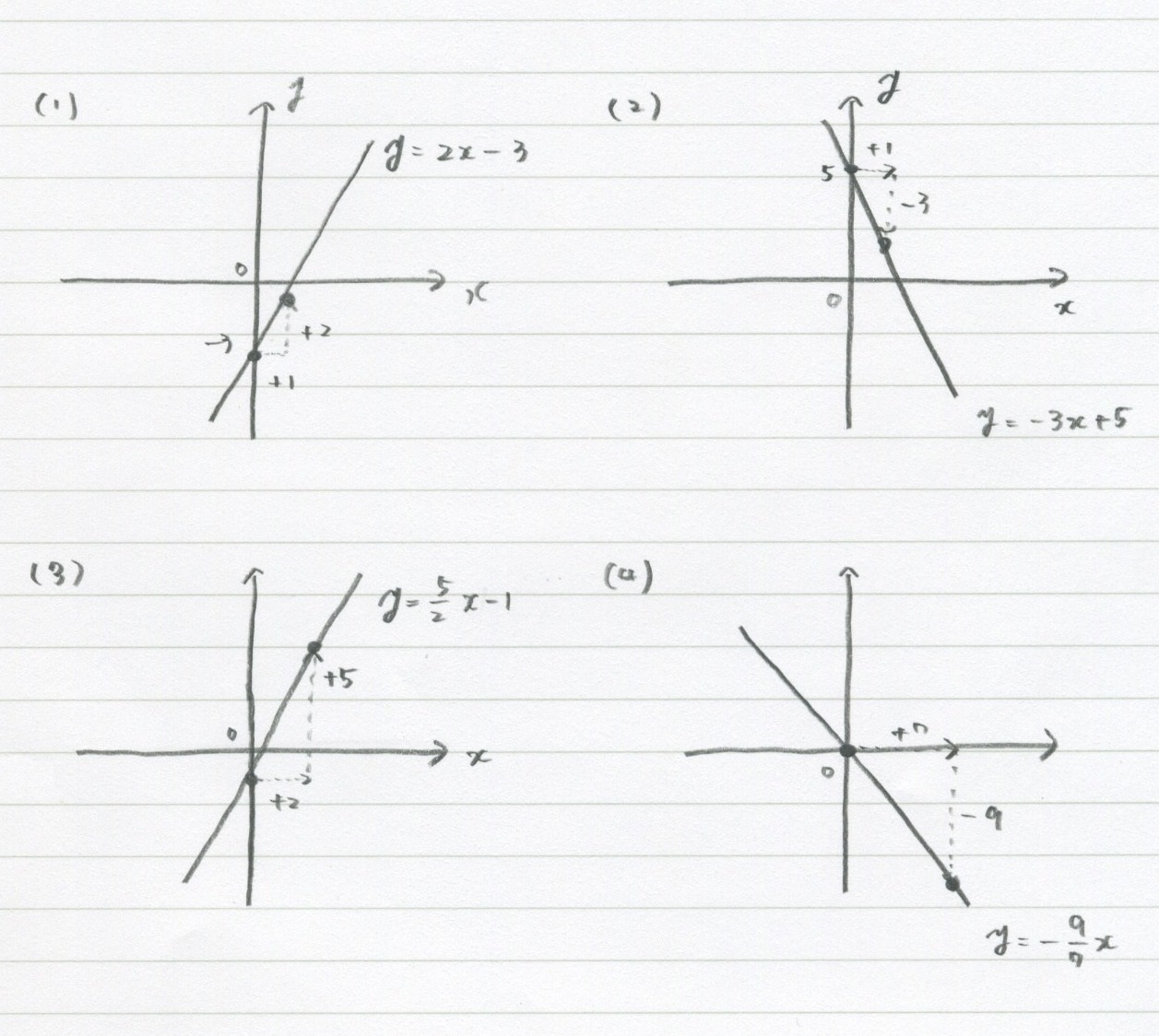 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
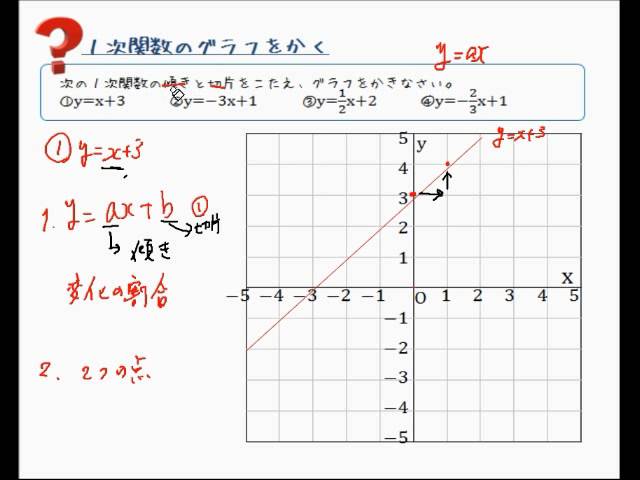 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 | 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
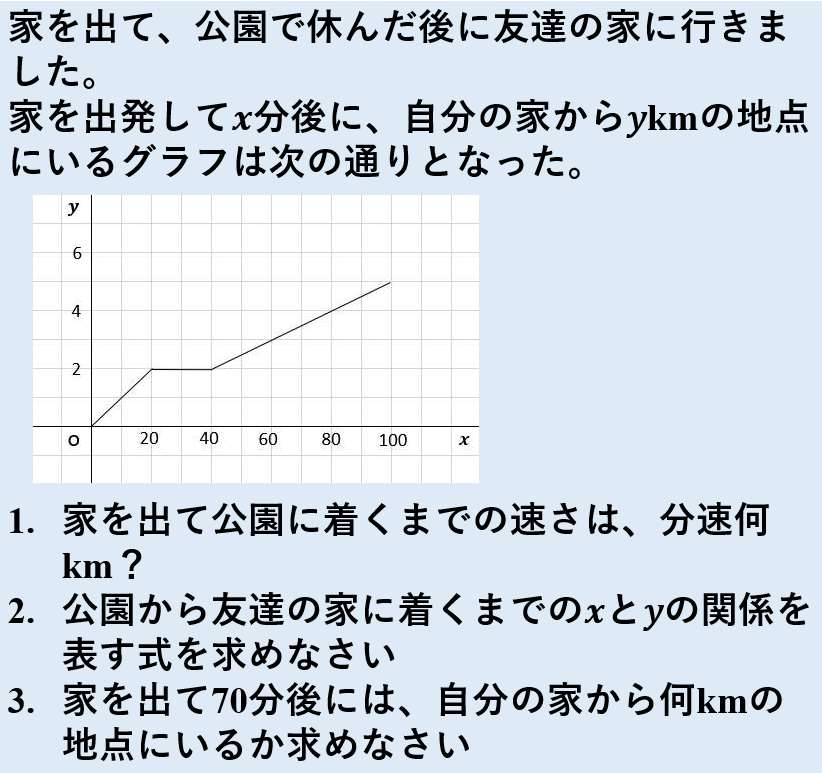 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 | 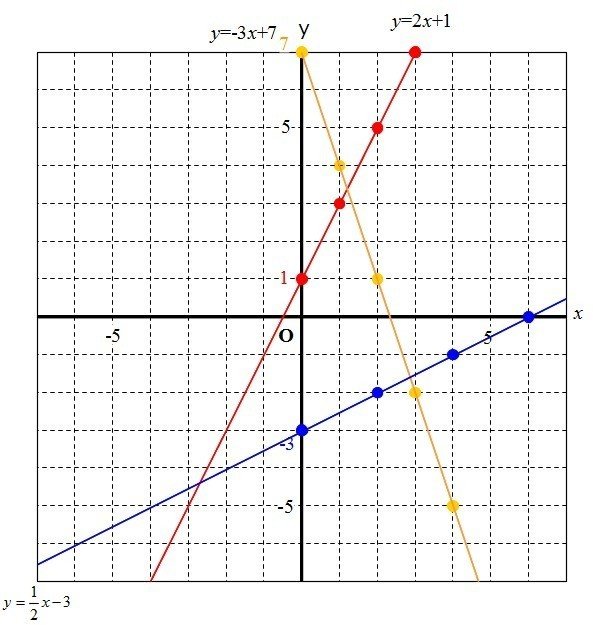 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
「1次関数 グラフ 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 | 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 | 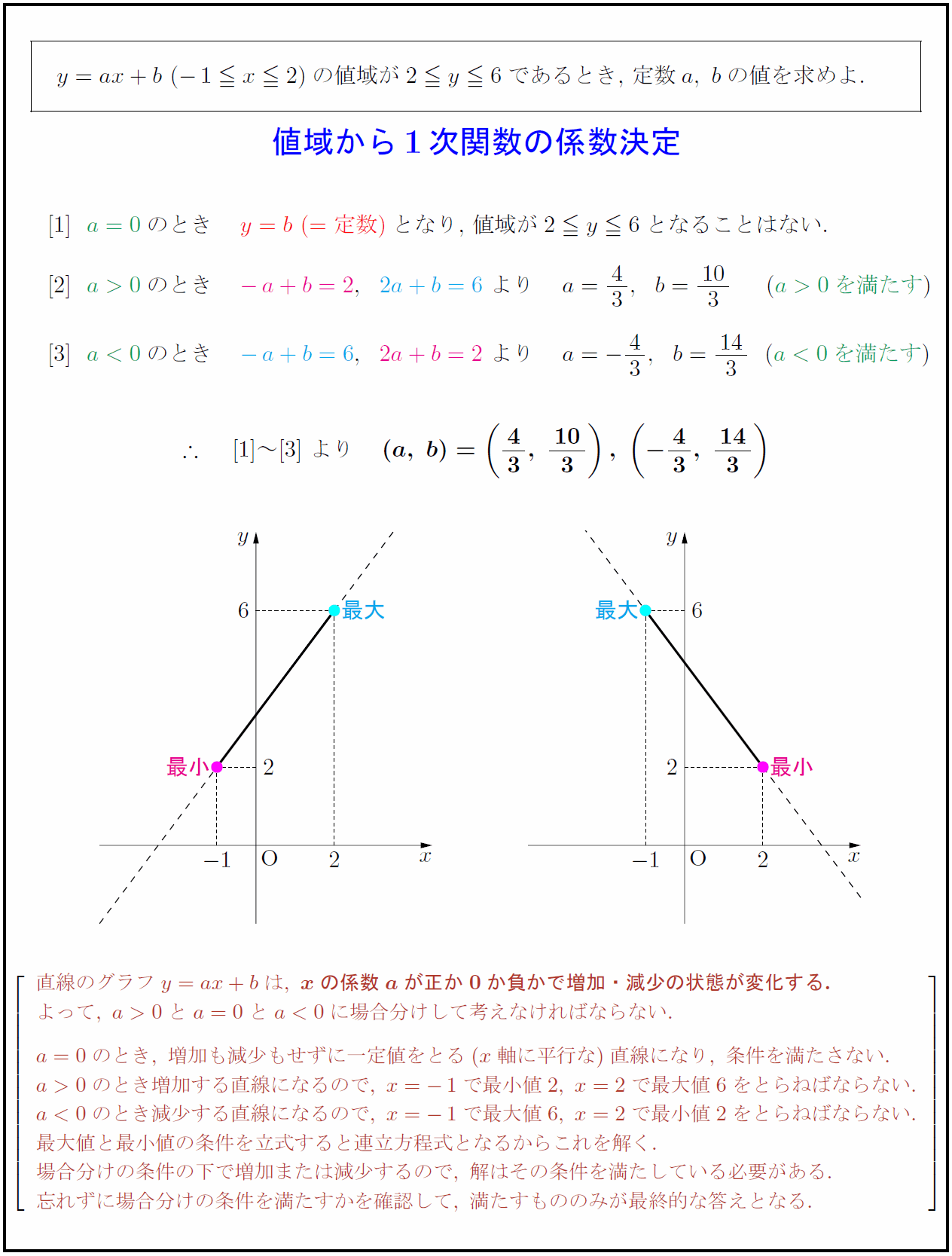 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
「1次関数 グラフ 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
「1次関数 グラフ 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 | 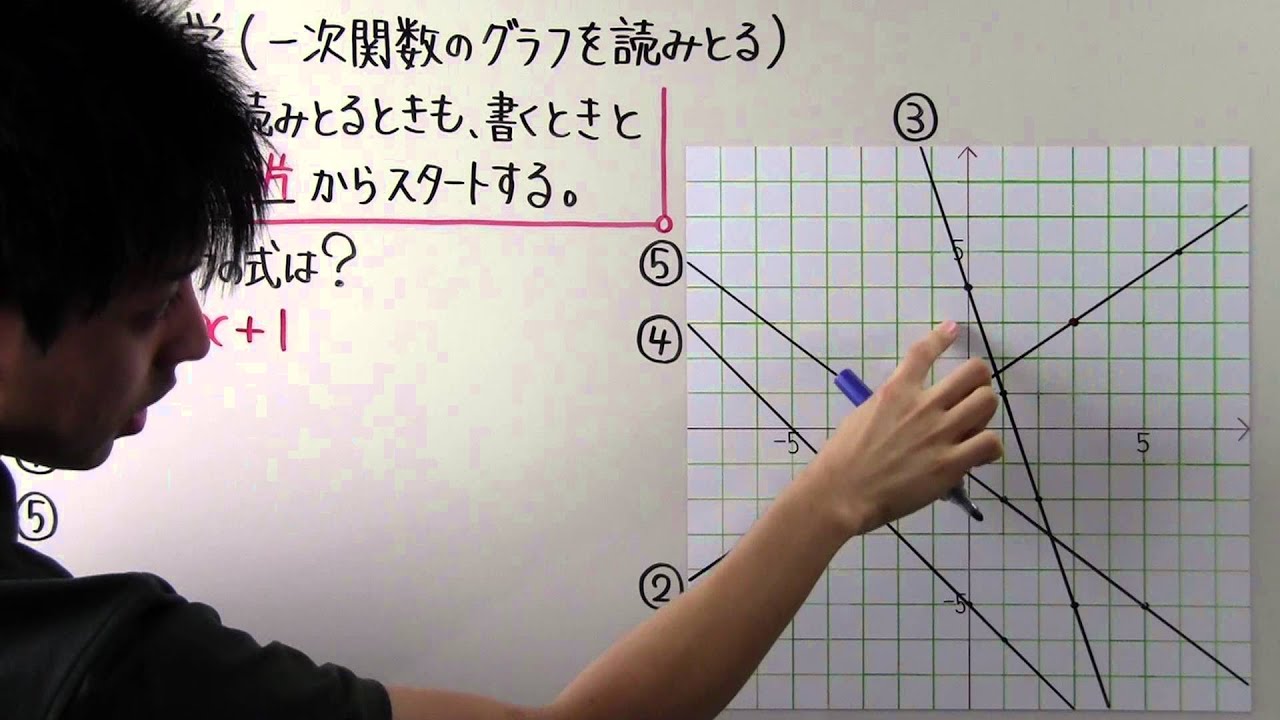 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
「1次関数 グラフ 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 | 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
「1次関数 グラフ 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
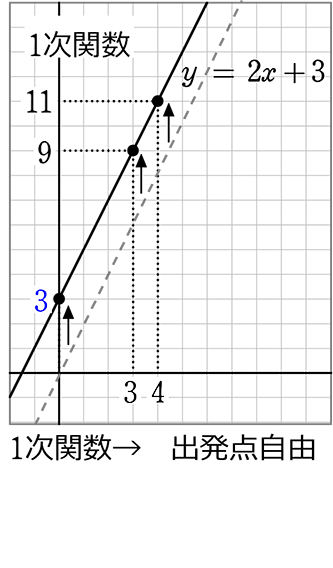 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 | 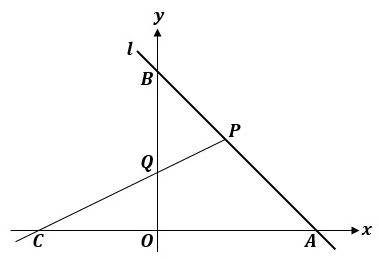 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |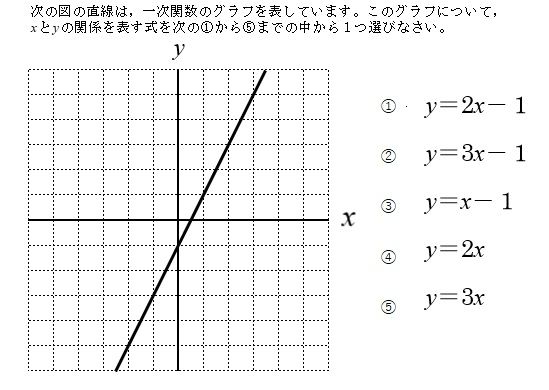
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 | 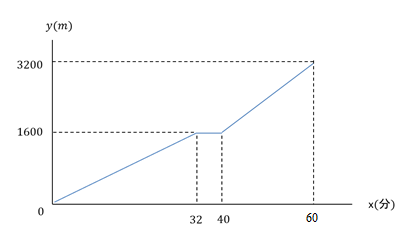 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
「1次関数 グラフ 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
「1次関数 グラフ 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
「1次関数 グラフ 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 | 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 | 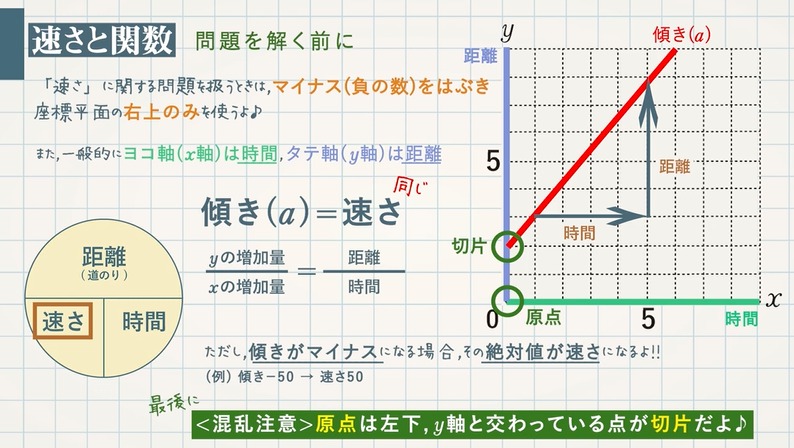 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
「1次関数 グラフ 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 | 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
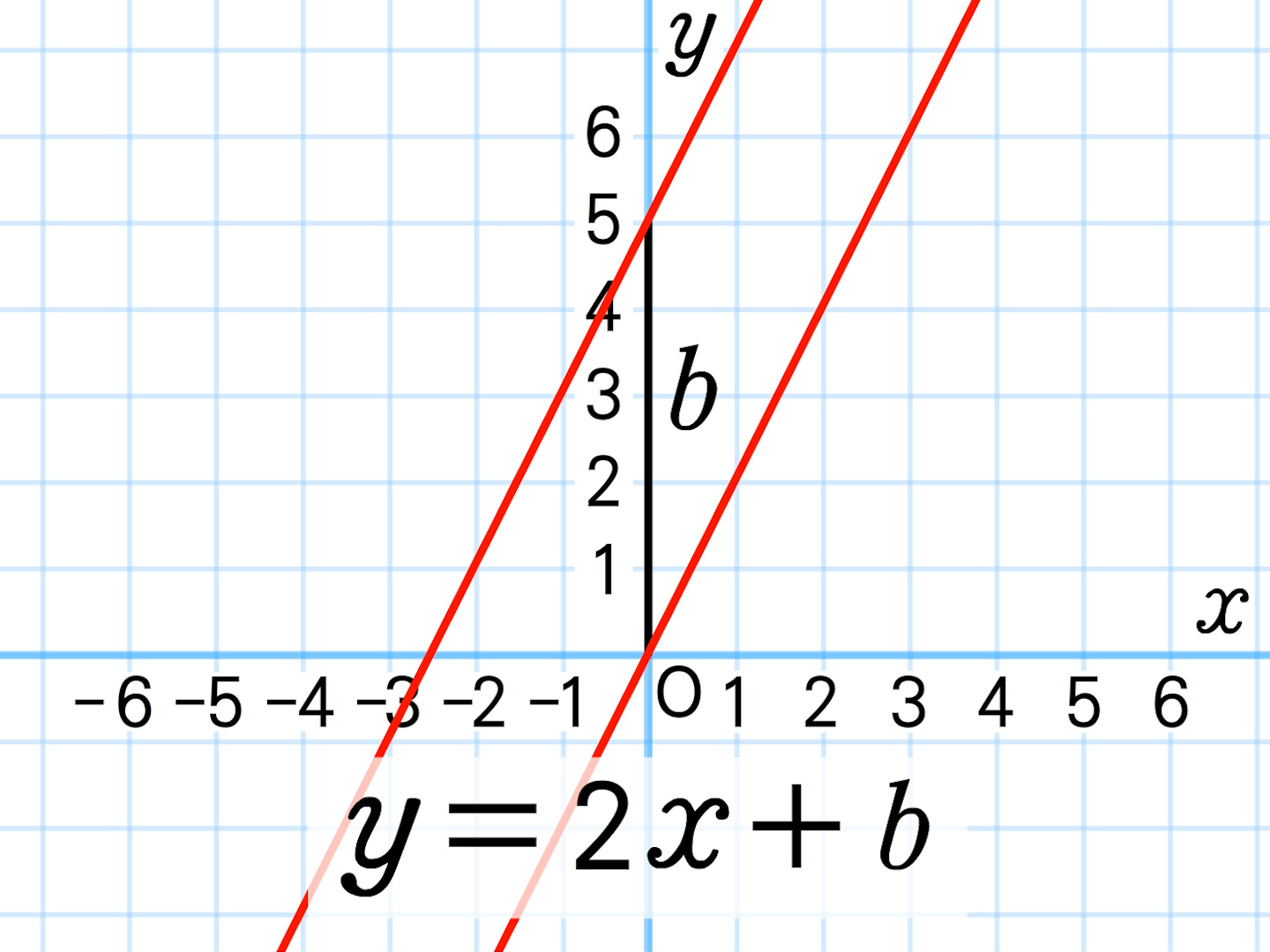 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 | 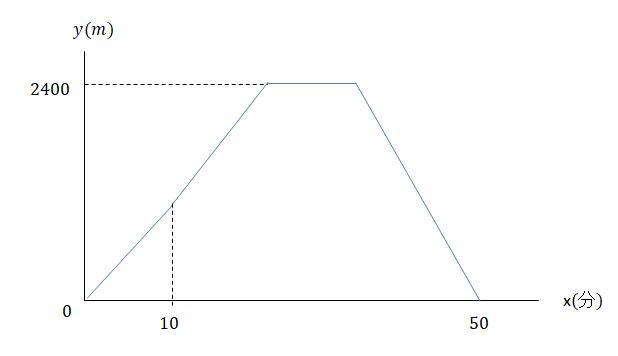 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
「1次関数 グラフ 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |  1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 | 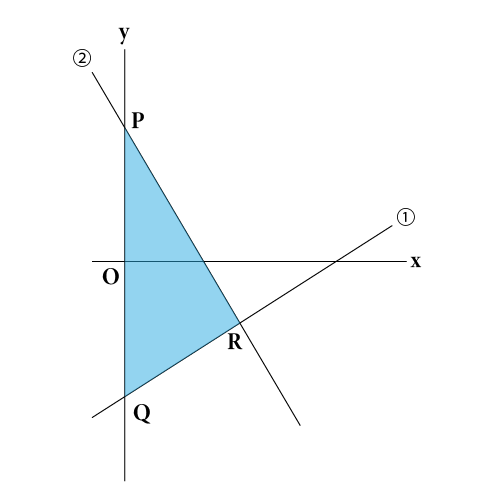 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 | 1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場 |
一次不等式を、グラフを使って解く 上の不等式を、次のようにグラフを使って考えてみましょう。 y = −2x 6 y = − 2 x 6 という直線を考えてみます。 また、例として x = 1,5 x = 1, 5 での点もとってみます。 x = 1 x = 1 のとき、この直線上の点は x 軸より上に 1次関数のグラフがかけたね^_^ まとめ：一次関数のグラフの書き方は「2点をむすぶ」だけ！ 一次関数のグラフはむずかしくない。 y軸との交点;
Incoming Term: 1次関数 グラフ, 1次関数 グラフ 問題, 1次関数 グラフ 求め方, 1次関数 グラフ 分数, 1次関数 グラフ サイト, 1次関数 グラフ 特徴, 1次関数 グラフ 傾き, 1次関数 グラフ 面積, 1次関数 グラフの利用, 1次関数 グラフ エクセル,
