負の数の平方根 √ (2)×√ (3) は通常 √ (2)i×√ (3)i = √ (6)i^2 = √ (6) と解きますが、 なぜ √ (2×3) = √ (6) としてはいけないのでしょうか。 よろしくお願いいたします。 ベストアンサー 数学・算数 負の数×負の数 負の数×負の数をよりわかりやすく 「負の平方根の中身の数字」というのは意味が取れないので、どういう意図か詳しく説明した方が良いと思います。例えば√(2) に対して i と虚数を出したい?それとも を返したい?平方根、符号付き平方根または逆平方根を計算するためのブロックへの入力信号。関数 sqrt は、複素数の固定小数点信号を除く実数入力または複素数入力を受け入れます。signedSqrt と rSqrt は複素数入力を受け入れません。 関数 signedSqrt では、入力信号は浮動小数点数でなければなりません。
高校入試の平方根をたった3分で 得意 にする方法 高校入試徹底対策ガイド
負の数の平方根はない
負の数の平方根はない- Pythonでルート (平方根)を計算するには、mathモジュールのsqrt関数を使います。 計算結果は無理数のため、有限の桁数しか扱えないコンピュータでは誤差が生じます。 厳密な計算をする場合には、計算精度にも注意します。 PR Pythonで挫折しない学習方法を複素数とは(負の数の平方根と虚数・複素数) 中学校では x 2 =−1 のような2次方程式の解は考えない 中学校で扱う数は実数と呼ばれ、数直線上に表示されるもので、2乗すれば必ず0以上になる。



2
方程式を解くときに(たとえばx2 3 = 0 のような)負の数の平方根が現れることに数学者が気がつ いたのは16 世紀のことでした.でも,i のような数は『ありえない』と考えて,imaginary number (日本語で虚数)と名づけました. 18 世紀後半になると複素数はむしろ自然なものとして扱われるよう No2 ベストアンサー 回答者: drum_KT 回答日時: 2138 答えはANo1の方の通りなのですが、この問題を理解するには「虚数」って何? というのを理解する必要があります。 まず、平方根とは何かを考えます。 √a というのは、これを二乗するとaになる数のことですよね。 (√a)^2 = a aがマイナスになるということは、二乗した時にマイナスになると 数学 負の平方根同士のかけ算が正の数にならない理由について、 複素幾何の方法ではなく、代数的方法で色々考えてみたのですが、 (a)^(1/2)・(b)^(1/2) = (a・b)^(1/2) が
累乗根について、もう少しくわしく 改めてかきますが、 この単元の学習の最終目標は指数関数 \(y=a^x\) なのです。 ※もうすぐ指数関数 \(y=a^x\) を学習します! 指数関数を扱うとき、有理数の指数法則の理解N n n が平方数でないときは m = n m m=\dfrac{n}{m} m = m n となる正の整数 m m m が存在しないので,全てペアになる。よって約数の個数は偶数。 なお,この考え方を使う問題が国際数学オリンピックで出題されたこともあります。 単に「約数」と言うと「負の数」を含むかどうかがあいまいです負の数の平方根は(実数の範囲には)ない。 2 つ目の項目について、2 乗して 0 になる数は 0 だけなので、0 の平方根は 0 の 1 つだけとなります。 3 つ目の項目について、2 乗して負になる数は(実数の範囲には)ないので、中学校の範囲では負の数の平方根はないとします。 しかし、複素数の範囲では、2 乗して 1 になる数 i が定義されているので、負の数の平方根
A 0で割算したり、負の数の平方根を求めようとしたような場合、 普通の数を答にするわけにいかない。 そこで、 指数フィールドが255の場合はそういう「数でないもの」を表すものと決めて、 それを答として返すことができるようにしてある。 C でプログラミングをするようになったら この様に負の数に平方根は存在しないということを必ず押さえておいて下さい。 答:無い では問題などで√4など、根号にマイナスがついている場合はどのように考えればよいのでしょうか。 この際は (1)×√4として考えます。 変数を勉強した際にaは1×a、aは1×aと学習したことと同じです。 平方根=根号では無いので注意しましょう。 負の数の平方根 a > 0 a > 0 のとき、 √−a = √ai − a = a i とする。 また、 −a − a の平方根は、 ±√ai ± a i とかける。 つまり、 √−3 = √3i − 3 = 3 i であり、 −8 − 8 の平方根は ±√−8 = ±2√2i ± − 8 = ± 2 2 i となります。




平方根とルートの違い ルート外しの注意点 趣味の大学数学



Www Kyoiku Shuppan Co Jp Textbook Chuu Sugaku Files Mathtb 3 2 Pdf
数学の平方根では、負の数の平方根を求めると虚数解が得られます。 しかし、Javaにはもともと虚数を表現する手段が含まれていません。 そのため、Mathクラスにある平方根を求めるsqrtメソッドの引数に負の数を与えると「NaN」が返されます。 これは、非数 (Not a Number)を表すビットパターンであり、Java以外の言語でも採用されている表記方法です。 ある値日本大百科全書(ニッポニカ) 平方根の用語解説 数aが与えられたとき、二乗(平方)してaとなる数、つまり、x2=aとなる数xをaの平方根という。aが正の数のときは、aの平方根は正の数、負の数それぞれ一つずつあり、その絶対値は等しい。そして、正のほうを、と書く。また、( ) 2 = 4 を成り立たせるような に入る数は無いので、 負の数の平方根は存在しない 平方根の数 正の数 ⇒ 平方根は正と負の2つ 0 ⇒ 0の平方根は0だけ 負の数 ⇒ 平方根は存在しない 文字のときの平方根




負の平方根 高校数学 Youtube



負の数の平方根は架空のもので存在しないというのはなぜですか Quora
負の数の平方根を用いない表現 虚数 は、 16世紀 のイタリアで、 三次方程式 を解く過程で発見された。 1637年 、 ルネ・デカルト は、複素数の虚部を " 仏 Nombre imaginaire "(「想像上の数」)と名付けた。長い間,1 の平方根が見つかりえないことは,議論の余地のな い真理であった.しかし,ルネッサンスのある時期に,勇気ある人々がこのタブー破ることもあった! √1 を書いても良い とすると,例えば, 2 3 √1 も書くことができるし, その意味をあまり考えないで形式的に計算をする数学Ⅱ ラジオ第2放送 毎週 水曜日・木曜日 午後7:50



負の数には平方根はない なぜですか 二乗してマイナスになる数字はな Yahoo 知恵袋




高校入試の平方根をたった3分で 得意 にする方法 高校入試徹底対策ガイド
どんな実数も自乗すると正の値、または、ゼロにしかならないからです。実数を自乗して負にすることはできません。したがって、負の数の平方根は架空の数です。 念のため、負の数を自乗すると必ず正の数になるという証明 正の数 matha/math を自乗した積 matha^2/math が正であるとの前提高校講座home >> 数学Ⅱ >> 第7回 第1章 方程式・式と証明 2次方程式 複素数(1) 負の数の平方根; 2乗してaになる数をaの 平方根 という。 正の数aの平方根は2つあり、絶対値が等しく符号が反対。 a と− a である。 0の平方根は0だけ、 0 =0 負の数の平方根は実数の範囲では存在しない。 a≧0のとき a >0、 (a) 2 = (− a) 2 = a a 2 = a つまり a≧0 なら a 2 = a a




数と式 平方根について 日々是鍛錬 ひびこれたんれん



1
Mathpow() 関数は base の exponent 乗、すなわち base exponent を返します。 base と exponent は10進数の数値です。 pow() は Math の静的メソッドなので、常に Mathpow() として使用し、自分で Math オブジェクトを生成してそのメソッドとして使用しないでください。 (Math にはコンストラクターがありません)。関数 sqrt の定義域には負の数と複素数が含まれており、意図せず使用すると予期しない結果になることがあります。 負の数と複素数 z = u i*w の場合、複素数の平方根 sqrt (z) は次を返します。 sqrt (r)* (cos (phi/2) 1i*sin (phi/2)) 「ルートの中は正(またはゼロ)でなければならない。」とよく言われます。 しかし、複素数(虚数)の計算ではルートの中が負になることがあります。 どういうことでしょうか? ルートの中は負の数でもよいのではないでしょうか? か



即日出荷 高校入試集中トレーニング数と式の計算 高校入試集中トレーニング 9 数学 書籍 全品送料無料 Www Simon Page Com




数と式 ルートの中が 負の数の2乗 のときの ルートのはずし方 数学 定期テスト対策サイト
累乗根 るいじょうこん root 方程式 x n =a(a は実数)を満足する x の値を,a の(正の)n 乗根といい,これを a 1/n と表す。 a の n 乗根の個数は,範囲を複素数にまで広げて考えれば一般に n 個ある。 a の n 乗根のうち実数値をとるものは,(1) a が正,n が偶数のとき ,(2) a が正,n が奇数の入力が負の数の場合、RuntimeWarning をスローし、結果として nan を返します。 コード例:複素数の numpysqrt() import numpy as np arr = 34j, 512j, 86j, 158j arr_sqrt = npsqrt(arr) print(arr_sqrt) 出力: 21j 23j 31j 14j 複素数には 2つの平方根があります。例えば、負の数 の平方根,すなわち の解は 異なる つの純虚数,互いに共役 を と表す, は 負の数 の約束 根号の規約




平方根とルート 根号 の概念 有理数と無理数の違い リョースケ大学




平方根が存在することをどう証明するか 解析学 第i章 実数と連続2
また少し意識しておくといいのが平方根は0以上の数にしかないということです。 (平方根の意味をきちんと理解しておけば当然かもしれませんが。) つまり、負の数の平方根はないということです。 2乗して負の数になるという数はありません。 2 Continue reading したがって、ルートとは同じ数を2回かけたものの根(元となるもの)という意味です。 0の平方根は0のみであり、どんな正の数aに対しても平方根は正と負の2つ存在し、 そのうち正である方を√を使って と表します。 つまり、 である必要があるのです。 point 複素数の平方根で有名な1=−1となるパラドックスを紹介. 実数の平方根と異なり,符号を一意に決められないことが原因. 高校生や大学の複素解析を学んだとき,「平方根」で混乱したことはないでしょうか?一見正しそうな計算により,1=−1 が導かれる原因について解説します.




数学の一問一答 平方根 勿忘荘



Http Yonominami J Saitama City Ed Jp Subj Suugaku Subj Math 3002 Pdf
平方根1_平方根を求める x 2 =A のとき xをAの 平方根 という。 正の数には平方根が2つ,0の平方根は0だけで,負の数には平方根はない, 解説動画 ≫ 次の数の平方根を求めよ。 25 1 4 6 ① 2乗して25になる数は 5と5なので数の範囲を,いままでみてきたような複素数にまで拡張すれば,負の数の平方根を求めることができる. 例として, − 3 の平方根を求めてみよう. つまり, − 3 の平方根は √3i と − √3i である. 一般には次のようにまとめられる.負の数の平方根を含んだ式にふつうの規則による計算を施した場合,負の数の平方根を含まない結果に到達することがある ことがわかってきた. 16 世紀にカルダノ(Cardano) は3 次方程式の根の公式を発見した.3 次方程式の3 根がすべて実根であるというまさ



Happylilac Net Pdf Jhs Math3 02 01ans Pdf



負の数の平方根は実数の集合に存在しないと表示されますが 実数以 Yahoo 知恵袋



負の数には平方根はない なぜですか 二乗してマイナスになる数字はな Yahoo 知恵袋



Http Www Fdtext Com Dat Suub3 2kon 1kon Pdf




2の平方根 Wikipedia
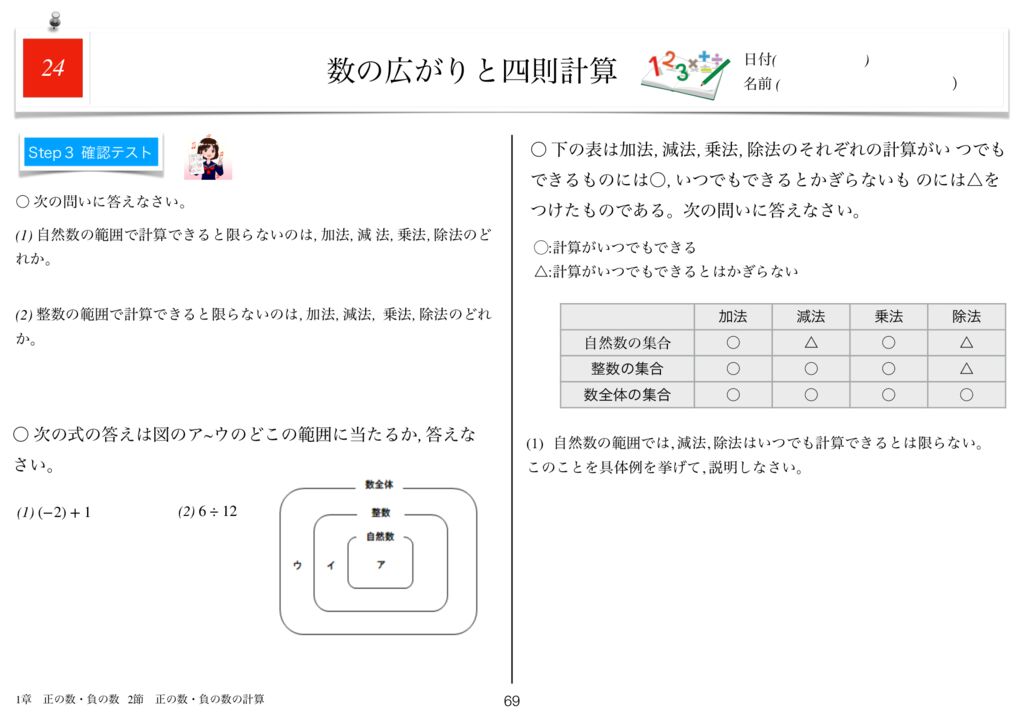



世界一わかりやすい数学問題集中1 1章 正の数 負の数



1




平方根の利用 2 整数部分小数部分 標 難 数学の解説と練習問題




負の数の平方根 Youtube




平方根とは すうがくのいえ




正の平方根ってなんですか 笑 よく分からないです 教えてくれる方いたら嬉しいです Clear




中学3年生 数学 平方根 問題プリント 無料ダウンロード 印刷 このページの答えのプリント 全部




中学の数学 平方根 を理解して受験を乗り切ろう 札幌市 学習塾 受験 チーム個別指導塾 大成会



自然数とは 1分でわかる意味 整数との違い ルート マイナスの数 0との関係




平方根 2乗するとaになる数 教遊者




どうして負の数かける負の数に意味があるのか ビデオ 負の数のかけ算と割り算 カーンアカデミー



負の数には平方根はない なぜですか 二乗してマイナスになる数字はな Yahoo 知恵袋




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ




中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ



2




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ




平方根とは すうがくのいえ




ひばりが丘校 常識を疑い 好奇心を育む 中学 高校 大学受験の朋友 学習塾のオフィシャルブログ




ルートなんて意味不明 の意味や特徴を理解しよう 平方根がない数ってあるの さびねこ中学校
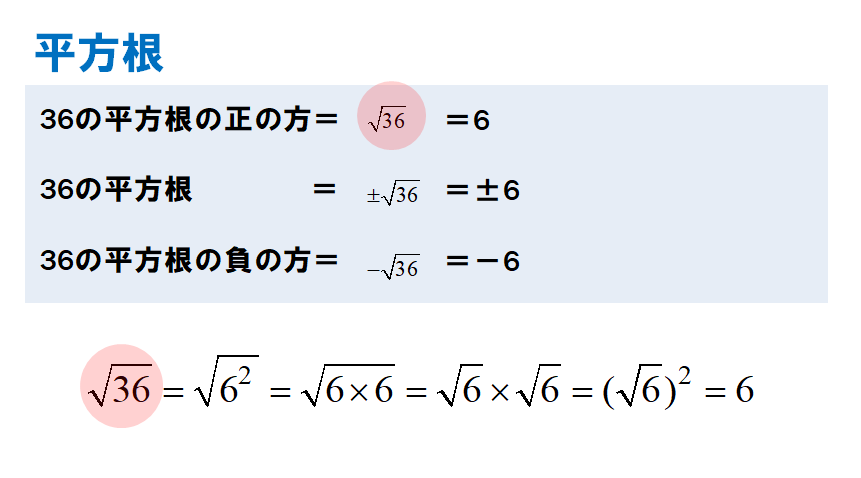



中3数学 平方根の性質の定期テスト対策問題 Examee




中3数学 平方根の定期テスト予想問題 Pikuu




数学 負の数の平方根の使い方とコツ 教科書より詳しい高校数学




なぜ ルート 平方根 の中身を足し算 引き算しちゃいけないの Qikeru 学びを楽しくわかりやすく



Http Www Kita9 Ed Jp Eductr Handbook Challengesheet Juniorhighschool Suugaku 3 2 Pdf




高1の数学でこんな感じに解の公式で の中がマイナスになった時にそのま 数学 教えて Goo




2重根号の計算 数学 苦手解決q A 進研ゼミ高校講座



知的断絶 の典型は何ですか Quora




平方根とは さわやか さくらぐみ




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ



高校入試の平方根をたった3分で 得意 にする方法 高校入試徹底対策ガイド
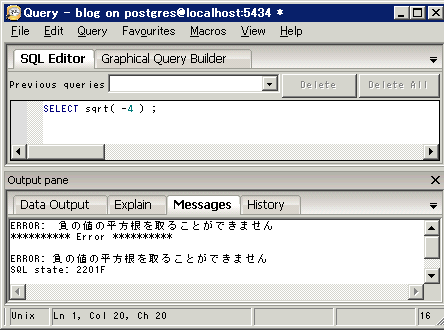



負の数の階乗がエラーにならない 研究に使うポスグレ




3 4 1 Mp4




これがわからないのですが 負の数は確かに二乗すると正の数となりますが そこからなぜ平 Clear




数と式 平方根について 日々是鍛錬 ひびこれたんれん




正の数と負の数 簡単な問題で 負の数の意味を覚えよう 中学や高校の数学の計算問題




ルートなんて意味不明 の意味や特徴を理解しよう 平方根がない数ってあるの さびねこ中学校




負の数の平方根 一夜漬け高校数学222 3の平方根は Youtube




数と式 平方根について 日々是鍛錬 ひびこれたんれん




ม 3 โน ตของ 中3数学 平方根まとめ ช น Junior High数学 Clear




平方根 2乗するとaになる数 教遊者




平方根 2 ルートと平方根の違い バカでもわかる 中学数学




これで完璧 平方根の基礎 中3数学 中学生の勉強法




平方根 Wikipedia




平方根はなぜプラスとマイナス両方あるの ルートの基本を確認 あんず学習塾のメモ 図表置き場




有理数から実数へ1 中学校3年の 平方根 の導入 身勝手な主張



1




北辰テスト対策 数学 平方根 蒼進塾 そうしんじゅく さいたま市 真剣に努力する姿勢を育む



2




これで完璧 平方根の基礎 中3数学 中学生の勉強法




正の数 負の数の加法 減法ゲーム 中学数学初級編 数学 統計教室の和から株式会社




数と式 平方根について 日々是鍛錬 ひびこれたんれん



Http Www Naka H Ibk Ed Jp Action Common Download Main Upload Id 2375




Python Sqrt で平方根 ルート を計算する フライテック




ゆうな 誰か平方根からその計算までみっちり教えてくれる人居ない 助けて 中三 数学



中学数学単元別 平方根 数学 中学校 教材 問題集 Buyee Buyee Japanese Proxy Service Buy From Japan Bot Online




平方根とは すうがくのいえ



2乗 平方根




中学数学 正負の数 でつまずく原因と解決法 乗除 累乗




平方根 2乗するとaになる数 教遊者



すみません 質問です 下の画像で どんな数を2乗しても負の Yahoo 知恵袋




高校 数学 複素数7 負の数の平方根 13分 Youtube



Www Kyoiku Shuppan Co Jp R3chuu Sugaku Files Dl11 Sugaku Pdf



3 25第2章1平方根 平方根とは 中学生



1
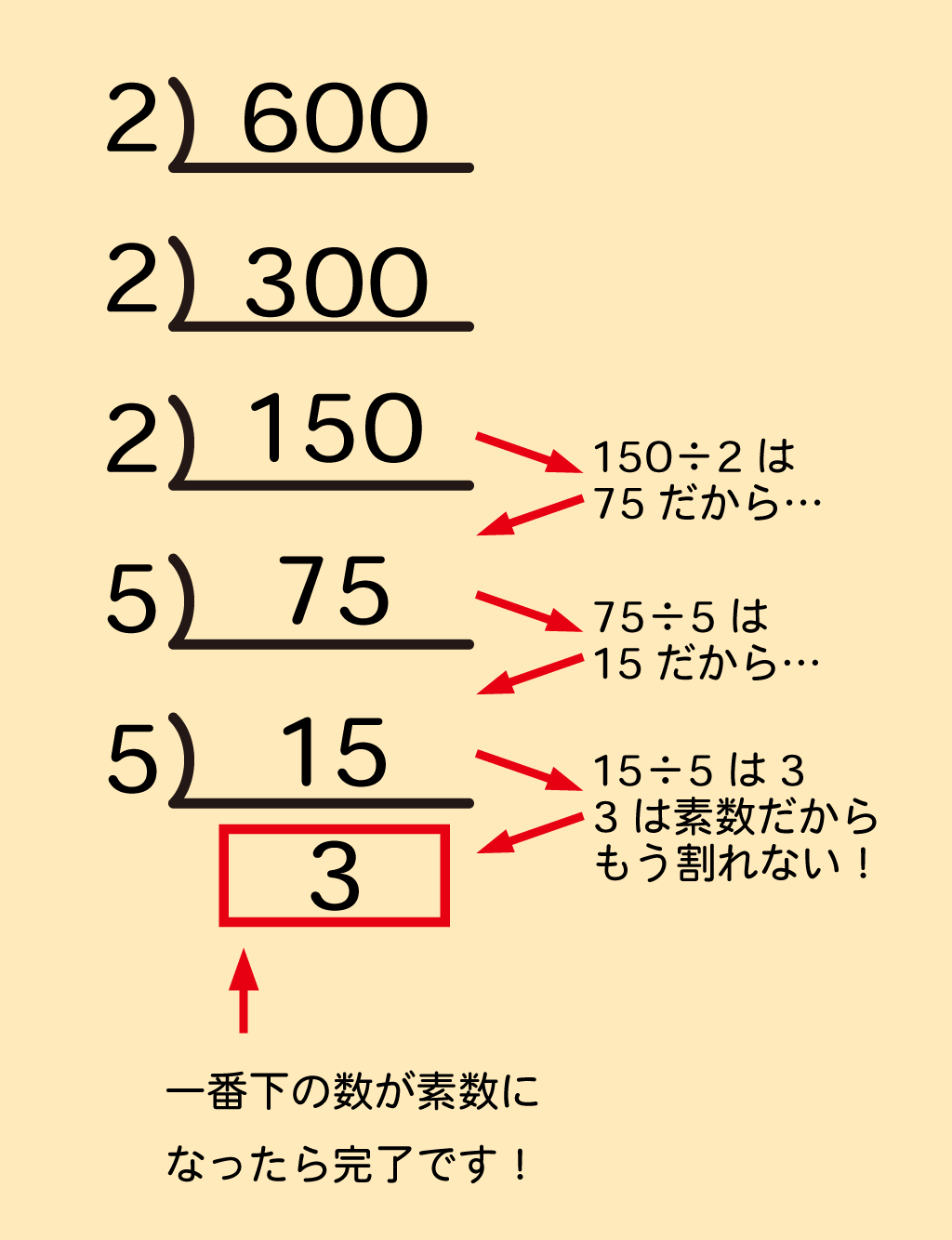



中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ
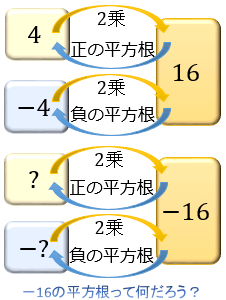



平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ




みぃか 5周年記念イラスト間に合わなさそうだから 落書き載せとくw るぅとinルート 実際の負の数の平方根 の解き方と違うとか言わないでw すとぷりギャラリー るぅとくん 腹黒 T Co Pvwiczfzcm Twitter
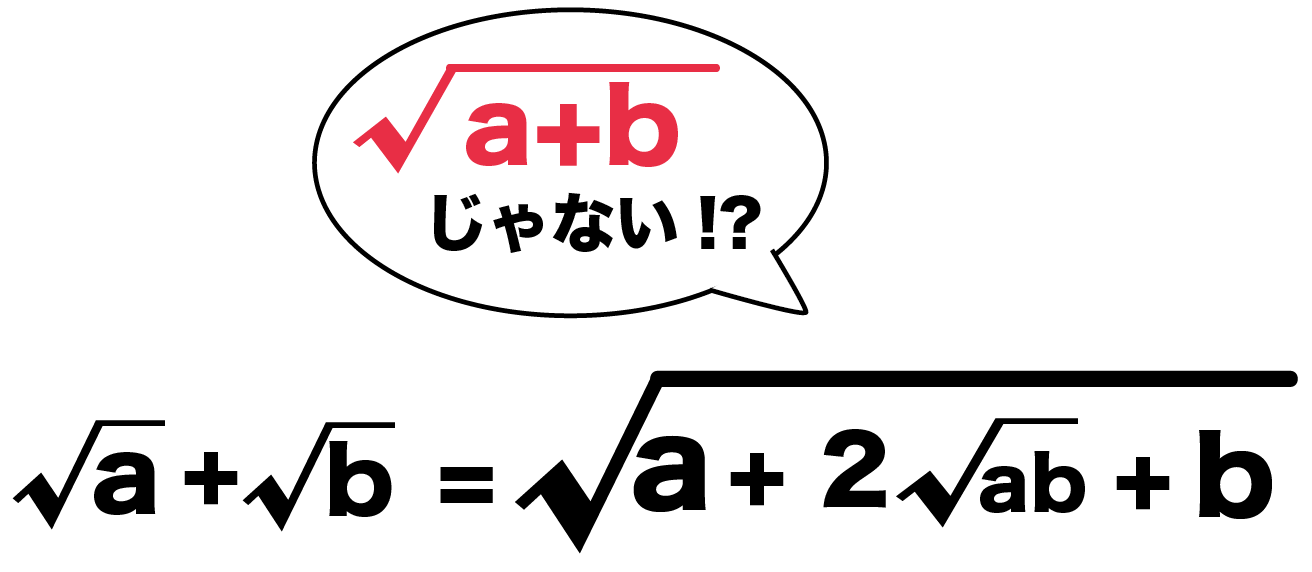



なぜ ルート 平方根 の中身を足し算 引き算しちゃいけないの Qikeru 学びを楽しくわかりやすく




Phpで数の平方根を見つける Men Of Letters メン オブ レターズ 論理的思考 業務改善 プログラミング




平方根はなぜプラスとマイナス両方あるの ルートの基本を確認 あんず学習塾のメモ 図表置き場




マーカーしてある部分なんですが 二乗して負になる数は無いのは分かるのですが それで何 Clear




数1の教科書です X 0のとき X 2 Xになぜなるのでしょうか Clear




メルカリ 中3 数学問題集 ビューポイント 参考書 400 中古や未使用のフリマ




正負の数 中学数学 By Okボーイ マナペディア




これで完璧 平方根の基礎 中3数学 中学生の勉強法
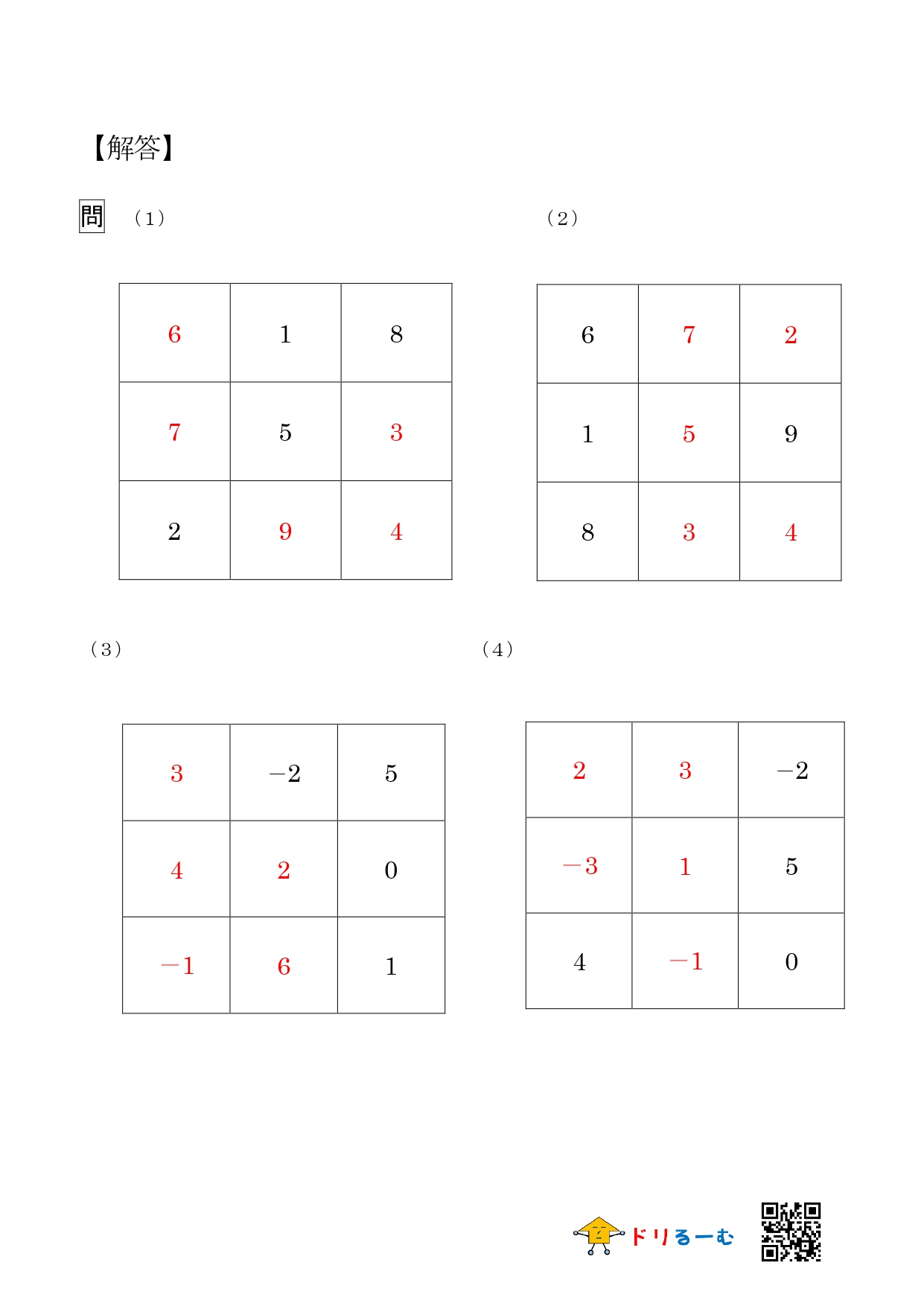



正の数 負の数 魔方陣 ドリるーむ




中学校3年分の数学が教えられるほどよくわかる なぜ を解決 の通販 小杉 拓也 紙の本 Honto本の通販ストア




中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ
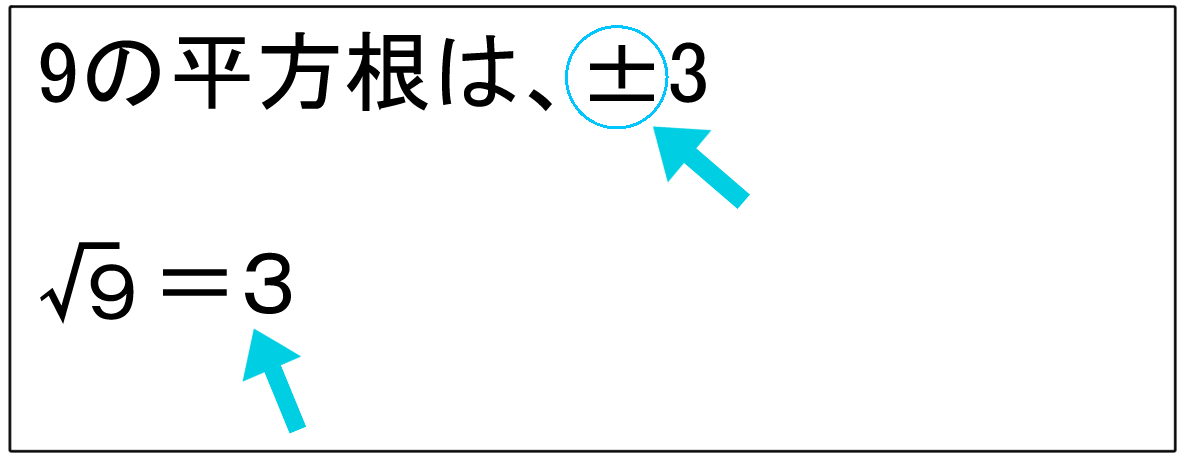



平方根 2 ルートと平方根の違い バカでもわかる 中学数学




平方根とルート 根号 の概念 有理数と無理数の違い リョースケ大学



2




平方根 1 きっずゼミ子育て応援ブログ



中学生の数学講座 負の数を使わないで表す




ルート64 8ではない のはなぜか 中学数学 定期テスト対策 ベネッセ教育情報サイト



Http Www Zkai Co Jp Ad Mihon Ikkan M Pdf


